Preprocessing of EO data - Radiometry
(EO4GEO - Faculty of Geodesy University of Zagreb)What is Preprocessing?
- In the context of digital analysis of remotely sensed data, preprocessing refers to those operations that are preliminary to the primary analysis (processing).
- Typical preprocessing operations could include:
- (1) radiometric preprocessing to adjust digital values for effects of a hazy atmosphere and/or
- (2) geometric preprocessing to bring an image into registration with a map or another image.
- Once corrections have been made, the data can then be subjected to the primary analyses.
- Preprocessing forms a preparatory phase that improves image quality.
Preprocessing facts
- It should be emphasized that: there can be no definitive list of “standard” preprocessing steps.
- The quality of image data varies greatly, so some data may not require the some type of preprocessing that would be necessary in other instances.
- Also, preprocessing alters image data!!!
- Although we may assume that such changes are beneficial, the analyst should remember that preprocessing may create artifacts that are not immediately obvious.
- The analyst should tailor preprocessing to the data at hand and the needs of specific projects
- Using only those preprocessing operations essential to obtain a specific result.
Preprocessing Operations
- Preprocessing operations, sometimes referred to as image restoration and rectification, are intended to correct for sensor- and platform-specific radiometric and geometric distortions of data.
- Radiometric corrections may be necessary due to variations in scene illumination and viewing geometry, atmospheric conditions, and sensor noise and response.
- Each of these will vary depending on the specific sensor and platform used to acquire the data and the conditions during data acquisition.
- Also, it may be desirable to convert and/or calibrate the data to known (absolute) radiation or reflectance units to facilitate comparison between data.
Geometric and Radiometric errors
- When image data is recorded by sensors on satellites and aircraft it can contain errors in geometry, and in the measured brightness values of the pixels.
- The second are referred to as radiometric errors and can result from
- the instrumentation used to record the data the wavelength dependence of solar radiation and
- the effect of the atmosphere.
- Geometric errors can also arise in several ways.
- the relative motions of the platform.
- non-idealities in the sensors themselves,
- the curvature of the earth and uncontrolled variations in the position,
- velocity and attitude of the remote sensing platform can all lead to geometric errors of varying degrees of severity.
Geometric and Radiometric errors (2)
- It is usually important to correct errors in image brightness and geometry.
- That is certainly the case if the image is to be as representative as possible of the scene being recorded.
- It is also important if the image is to be interpreted manually.
- If an image is to be analysed automaticali (by machine), using the specific algorithms, it is not always necessary to correct the data beforehand;
- that depends on the analytical technique being used.
- Some institutions (experts) of thought recommend against correction when analysis is based on pattern recognition methods.
Instrumentation Radiometric Errors
- Mechanisms that affect the measured brightness values of the pixels in an image can lead to two broad types of radiometric distortion.
- First, the distribution of brightness over an image in a given band can be different from that in the ground scene.
- Secondly, the relative brightness of a single pixel from band to band can be distorted compared with the spectral reflectance character of the corresponding region on the ground.
- Both types can result from the presence of the atmosphere as a transmission medium through which radiation must travel from its source to the sensors, and can also be the result of instrumentation effects.
Sources of Radiometric Distortion (1)
- An ideal detected radiation should be linear.
- Real detectors will have some degree of non-linearity.
- There will also be a small signal out, even when there is no radiation in.
- Historically that is known as dark current and is the result of residual electronic noise present in the detector at any temperature other than absolute zero.
- In remote sensing it is usually called a detector offset.
- The slope of the detector curve is called its gain, or sometimes transfer gain.
Sources of Radiometric Distortion (2)
- An ideal radiation detector has a transfer characteristic such as that shown in Figure a.

a) Linear radiation detector transfer characteristic, and
b) hypothetical mismatches in detector characteristics
How dark current can be recorded?
Sources of Radiometric Distortion (3)
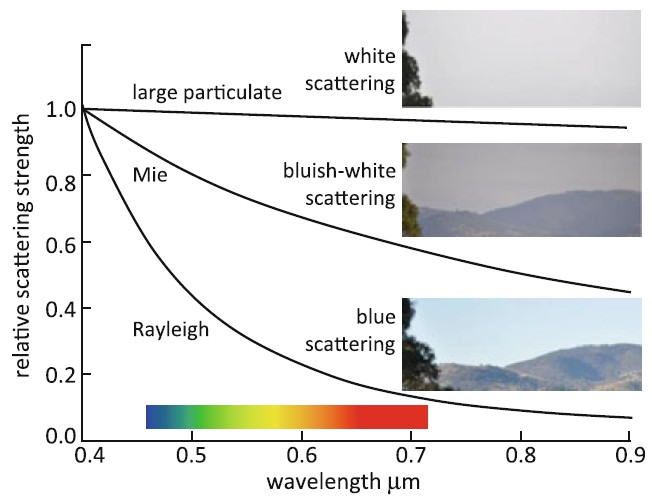
Atmospheric and particulate scattering.
Sources of Radiometric Distortion (4)
- Most imaging devices used in remote sensing are constructed from sets of detectors.
- In the case of the Landsat ETM+ there are 16 per band.
- Each will have slightly different transfer characteristics, such as those depicted in previous Figure b.
- Those imbalances will lead to striping in the across swath direction.
- For push broom scanners there are as many as 12,000 detectors across the swath in the panchromatic mode of operation.
- For monolithic sensor arrays that is rarely a problem, compared with the line striping that can occur with mechanical across track scanners that employ discrete detectors.
Sources of Radiometric Distortion (5)
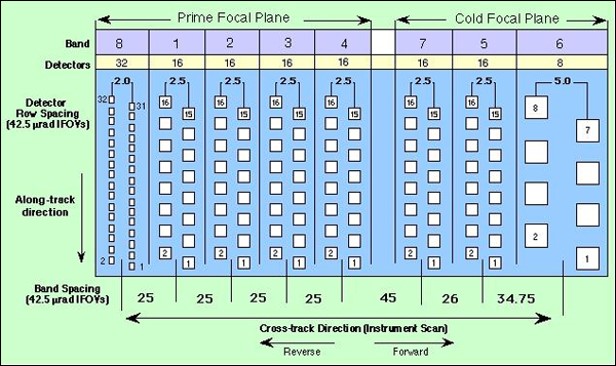
Landsat-7 detector projection at the prime focal plane.
Bands: 1) 0.45 - 0.52 VNIR; 2) 0.52 - 0.60 VNIR; 3) 0.63 - 0.69 VNIR; 4) 0.76 - 0.90 VNIR; 5) 1.55 - 1.75 SWIR; 7) 2.08 - 2.35 SWIR; 6) 10.4 - 12.5 TIR
Sources of Radiometric Distortion (6)
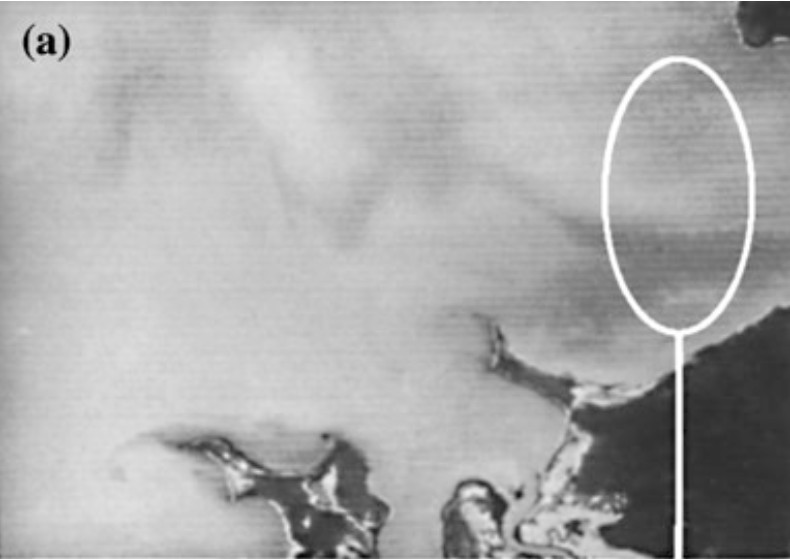
Original Landsat MSS image with striping noise.
Sources of Radiometric Distortion (7)
- Another common instrumentation error is the loss of a complete line of data resulting from a momentary sensor or communication link failure, or the loss of signal on individual pixels in a given band owing to instantaneous drop out of a sensor or signal link.
- Those mechanisms lead to black lines across or along the image, depending on the sensor technology used to acquire the data, or to individual black pixels.
Correcting Instrumentation Errors
- Errors in relative brightness can be rectified to a great extent in the following way.
- First, it is assumed that the detectors used for data acquisition in each band produce signals statistically similar to each other.
- If the means and standard deviations are computed for the signals recorded by each of the detectors over the full scene then they should almost be the same.
- This requires the assumption that statistical detail within a band doesn’t change significantly over a distance equivalent to that of one scan covered by the set of the detectors.
- For most scenes this is usually a reasonable assumption in terms of the means and standard deviations of pixel brightness.
Correcting Instrumentation Errors: Striping (1)
- Optical/mechanical scanners are subject to a kind of radiometric error known as striping, or dropped scan lines, which appear as a horizontal banding caused by small differences in the sensitivities of detectors within the sensor.
- Within a given band, such differences appear on images as banding where individual scan lines exhibit unusually brighter or darker brightness values that contrast with the background brightnesses of the “normal” detectors.
- Sensor mismatches of this type can be corrected by calculating pixel mean brightness and standard deviation using lines of image data known to come from a single detector.
Correcting Instrumentation Errors: Striping (2)
- Within the Landsat MSS this error is known as sixth-line striping due to the design of the instrument.
- Because MSS detectors are positioned in arrays of six, an anomalous detector response appears as linear banding at intervals of six lines.
- In the case of Landsat MSS that will require the data on every sixth line to be used.
- In a like manner five other measurements of mean brightness and standard deviation are computed for the other five MSS detectors.
Correcting Instrumentation Errors: Striping - Example
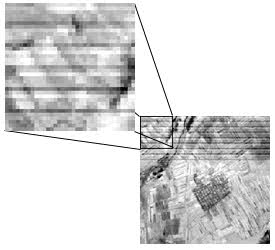
Line striping in Landsat MSS data.
Correcting Instrumentation Errors: Striping (3)
- Correction of radiometric mismatches among the detectors can then be carried out by adopting one sensor as a standard and adjusting the brightnesses of all pixels recorded by each other detector.
- This operation is called destriping.
- Destriping refers to the application of algorithms to adjust incorrect brightness values to values thought to be near the correct values.
- Some image processing software provides special algorithms to detect striping.
 |
Correcting Instrumentation Errors: Striping – ExamplesReducing sensor induced striping noise in a Landsat MSS image: a) original image, and b) after destriping by matching sensor statistics.
|
Correcting Instrumentation Errors: Striping (4)
- A variety of destriping algorithms have been devised.
- All identify the values generated by the defective detectors by searching for lines that are noticeably brighter or darker than the lines in the remainder of the scene.
- Then the destriping procedure estimates corrected values for the bad lines.
- There are many different estimation procedures; most belong to one of two groups.
Correcting Instrumentation Errors: Striping (5)
- One approach - replaceing bad pixels with values based on the average of adjacent pixels not influenced by striping
- this approach is based on the notion that the missing value is probably quite similar to the pixels that are nearby.
- A second strategy is to replace bad pixels with new values based on the mean and standard deviation of the band in question or on statistics developed for each detector.
- Second approach - based on the assumption that the overall statistics for the missing data must resemble those from the good detectors.
Correcting Instrumentation Errors: Striping - Example
 |
Two strategies for destriping.
|
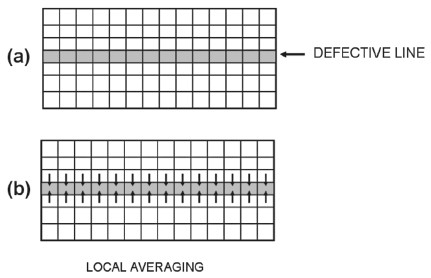
Correcting Instrumentation Errors: Infilling
- Correcting lost lines of data or lost pixels can be carried out by averaging over the neighbouring pixels
- using the lines on either side for line drop outs or the set of surrounding pixels for pixel drop outs.
- This is called infilling or sometimes in-painting.
 |
Correcting Instrumentation Errors: Infilling - Examples
|
Radiometric Preprocessing (1)
- Radiometric preprocessing influences the brightness values of an image to correct for sensor malfunctions or to adjust the values to compensate for atmospheric degradation.
- Any sensor that observes the Earth’s surface using visible or near visible radiation will record a mixture of two kinds of brightnesses:
- the brightness derived from the Earth’s surface — that is, the brightnesses that are of interest for remote sensing.
- the sensor also observes the brightness of the atmosphere itself —the effects of atmospheric scattering.
- Thus an observed digital brightness value (e.g., “56”) might be in part the result of surface reflectance (e.g., “45”) and in part the result of atmospheric scattering (e.g., “11”).
Radiometric Preprocessing (2)
- Of course we cannot immediately distinguish between the two brightnesses.
- So, one objective of atmospheric correction is to identify and separate these two components.
- Ideally, atmospheric correction should find a separate correction for each pixel in the scene.
- In practice, we may apply the same correction to an entire band or apply a single factor to a local region within the image.
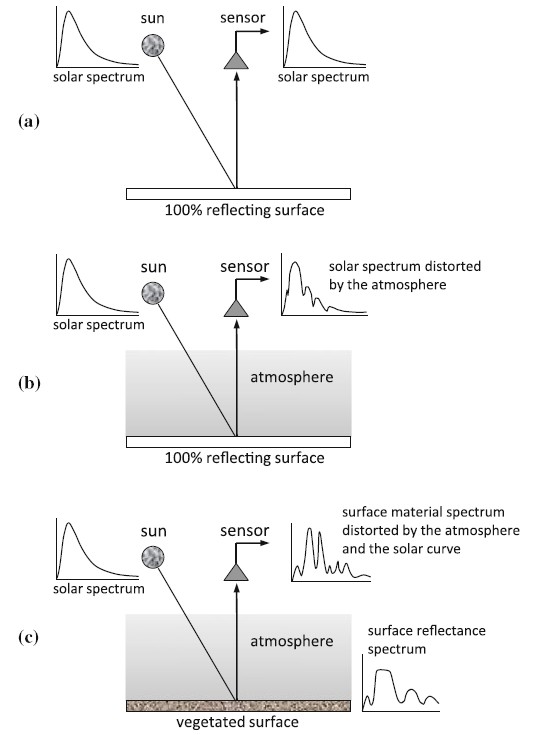 |
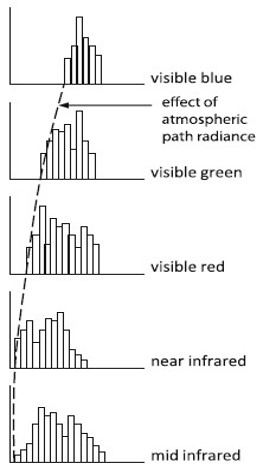
Solar Curve and the Effect of the AtmosphereDistortion of the surface material reflectance spectrum by the spectral dependence of the solar curve and the effect of the atmosphere:
|
Compensating for the Solar Radiation Curve (1)
- The wavelength dependence of the radiation falling on the Earth’s surface can be compensated by assuming that the Sun is an ideal black body.
- For images recorded by instrumentation with fine spectral resolution
- it is important to account for departures from black body behaviour,
- effectively modelling the real emissivity of the sun, and
- using that to normalise the recorded image data.
- Most radiometric correction procedures compensate for the solar curve using the actual wavelength dependence measured above the atmosphere.
Compensating for the Solar Radiation Curve (2)

Measured solar spectral irradiance of the sun above the Earth’s atmosphere over the wavelength range common in optical remote sensing.
Preprocessing operations: Radiative Transfer Code (1)
- Preprocessing operations to correct for atmospheric degradation fall into three rather broad categories.
- First - procedures known as radiative transfer code (RTC) computer models.
- Application of such models permits observed brightnesses to be adjusted to approximate true values that might be observed under a clear atmosphere
- thereby improving image quality and accuracies of analyses.
- RTC models the physical process of scattering at the level of individual particles and molecules,
- this approach has important advantages with respect to rigor, accuracy, and applicability to a wide variety of circumstances.
Preprocessing operations: Radiative Transfer Code (2)
- RTC also have significant disadvantages.
- Often they are complex, usually requiring detailed in situ data acquired simultaneously with the image and/or satellite data describing the atmospheric column at the time and place of acquisition of an image.
- Such data may be difficult to obtain in the necessary detail and may apply only to a few points within a scene.
- Although meteorological satellites collect atmospheric data that can contribute to atmospheric corrections of imagery.
Preprocessing operations: Image-based Atmospheric Correction (1)
- A second approach based on examination of spectra of objects of known or assumed brightness recorded by multispectral imagery.
- From basic principles of atmospheric scattering - scattering is related to wavelength, sizes of atmospheric particles, and their abundance.
- If a known target is observed using a set of multispectral measurements, the relationships between values in the separate bands can help assess atmospheric effects.
- This approach is often known as “image-based atmospheric correction”.
Preprocessing operations: Image-based Atmospheric Correction (2)
- Ideally, the target consists of a natural or man-made feature that can be observed with airborne or ground-based instruments at the time of image.
- However, in practice we seldom have such measurements, and therefore we must look for features of known brightness that commonly, or fortuitously, appear within an image.
- In its simplest form, this strategy can be implemented by identifying a very dark object or feature within the scene.
Preprocessing operations: Image-based Atmospheric Correction (3)
- Such an object might be a large water body or possibly shadows cast by clouds or by large topographic features.
- In the infrared portion of the spectrum, both water bodies and shadows should have brightness at or very near zero.
- Analysts who examine such areas, or the histograms of the digital values for a scene, can observe that the lowest values are not zero but some larger value.
- Typically, this value will differ from one band to the next.
Preprocessing operations: Dark Object Subtraction
- These values, assumed to represent the value contributed by atmospheric scattering for each band, are then subtracted from all digital values for that scene and that band.
- Thus the lowest value in each band is set to zero,
- the dark black color assumed to be the correct tone for a dark object in the absence of atmospheric scattering.
- Direct methods for adjusting digital values for atmospheric degradation - known sometimes as the histogram minimum method (HMM) or the dark object subtraction (DOS) technique.
- The haze will be removed and the dynamic range of image intensity will be improved.
- Consequently this approach is also frequently referred to as haze removal.
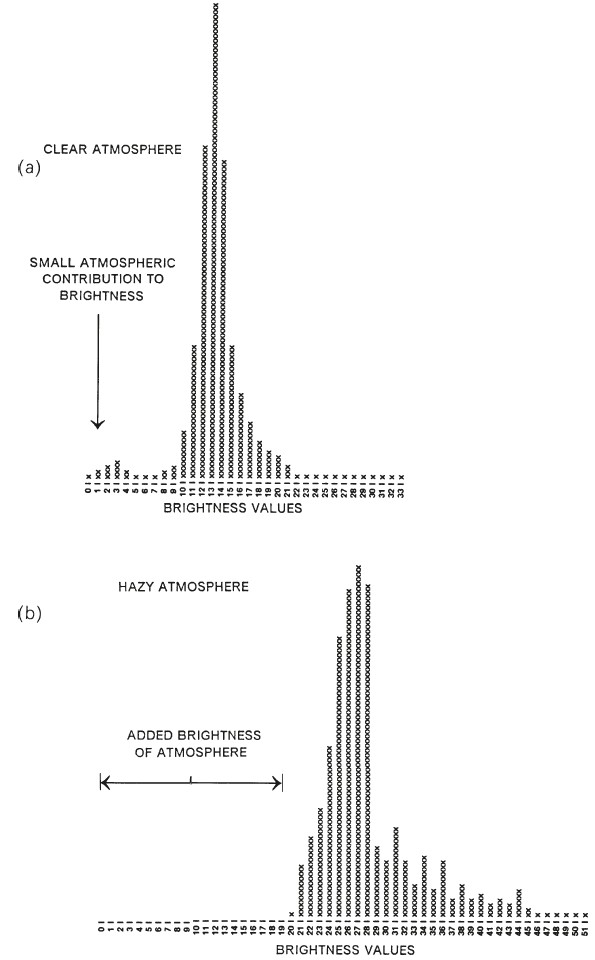 |
Preprocessing operations: Dark Object Subtraction (2)Histogram minimum method for correction of atmospheric effects. The lowest brightness value in a given band is taken to indicate the added brightness of the atmosphere to that band and is then subtracted from all pixels in that band.
|
Preprocessing operations: Dark Object Subtraction (3)
- This procedure has the advantages of simplicity, directness, and almost universal applicability.
- Yet it must be considered as an approximation;
- atmospheric effects change not only the position of the histogram on the axis but also its shape.
- The atmosphere can cause dark pixels to become brighter and bright pixels to become darker.
- Thus, the DOS technique is capable of correction for additive effects of atmospheric scattering, but not for multiplicative effects.
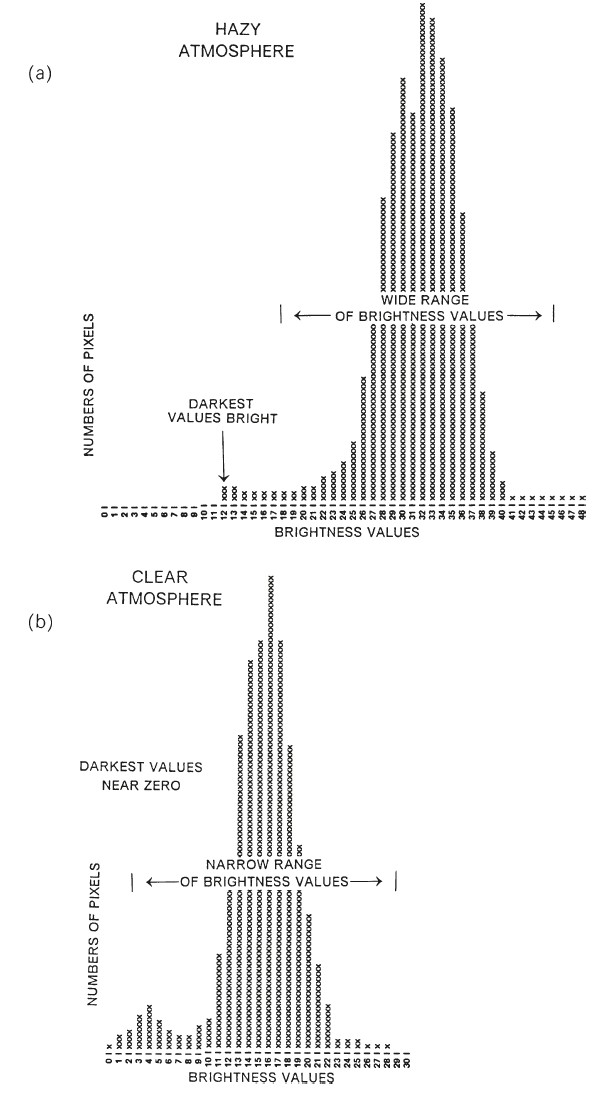 |
Inspection of histograms for evidence of atmospheric effects. |
Preprocessing operations: Dark Object Subtraction (5)
- Although DOS is the least accurate of the other methods
- its simplicity and the prospect of pairing it with other strategies might form the basis for a practical technique for operational use.
- Subtraction of a constant from all pixels in a scene will have a larger proportional impact on the spectra of dark pixels than on brighter pixels
- Users should apply caution in using it for scenes in which spectral characteristics of dark features.
- Despite such concerns, the technique, both in its basic form and in the various modifications, has been found to be satisfactory for a variety of remote sensing applications.
Preprocessing operations: Regression Technique
- A more sophisticated approach retains the idea of examining brightness of objects within each scene but attempts to exploit knowledge of interrelationships between separate spectral bands.
- Chavez (1975) devised a procedure that paired values from each band with values from a near infrared spectral channel.
- Whereas the HMM procedure is applied to entire scenes or to large areas
- the regression technique can be applied to local areas, ensuring that the adjustment is tailored to conditions important within specific regions.
Preprocessing operations: Covariance Matrix Method
- An extension of the regression technique is to examine the variance–covariance matrix.
- This is the covariance matrix method [CMM].
- Both procedures assume that within a specified image region, variations in image brightness are due to topographic irregularities and reflectivity is constant.
- Therefore, variations in brightness are caused by small-scale topographic shadowing, and the dark regions reveal the contributions of scattering to each band.
- Although these assumptions may not always be strictly met.
Advanced Atmospheric Correction Tools: MODTRAN
- MODTRAN (MODerate resolution atmospheric TRANsmission) is a computer model for estimating atmospheric transmission of electromagnetic radiation under specified conditions.
- MODTRAN estimates atmospheric emission, thermal scattering, and solar scattering, incorporating effects of molecular absorbers and scatterers, aerosols, and clouds for wavelengths from the ultraviolet region to the far infrared.
- It uses various standard atmospheric models based on common geographic locations and also permits the user to define an atmospheric profile with any specified set of parameters.
- The model offers several options for specifying prevailing aerosols, based on common aerosol mixtures encountered in terrestrial conditions.
- Within MODTRAN, the estimate of visibility serves as an estimate of the magnitude of atmospheric aerosols.
Calculating Radiances from DNs (1)
- Digital data formatted for distribution to the user community present pixel values as digital numbers (DNs),
- expressed as integer values to facilitate computation and transmission and to scale brightnesses for convenient display.
- Although DNs have practical value.
- They do not present brightnesses in the physical units necessary to understand the optical processes.
- When image brightnesses are expressed as DNs, each image becomes an individual entity
- without a defined relationship to other images or to features on the ground.
Calculating Radiances from DNs (2)
- DNs express accurate relative brightnesses within an image but cannot be used to examine brightnesses over time
- to compare brightnesses from one instrument to another, to match one scene with another, nor to prepare mosaics of large regions.
- DNs cannot serve as input for models of physical processes in (for example) agriculture, forestry, or hydrology.
- Therefore, conversion to radiances forms an important transformation to prepare remotely sensed imagery for subsequent analyses.
Calculating Radiances from DNs (3)
- DNs can be converted to radiances using data derived from the instrument calibration provided by the instrument’s manufacturer.
- Because calibration specifications can drift over time, recurrent calibration of aircraft sensors is a normal component of operation and maintenance.
- However, satellite sensors, once launched, are unavailable for recalibration in the laboratory
- although their performance can be evaluated by directing the sensor to view onboard calibration targets or by imaging a flat, uniform landscape, such as carefully selected desert terrain.
Calculating Radiances from DNs (4)
- For a given sensor, spectral channel, and DN, the corresponding radiance value (L) can be calculated as:
L = [(Lmax – Lmin)/(Qcalmax – Qcalmin)] × (Qcal – Qcalmin) + Lmin)
- where:
- L is the spectral radiance at the sensor’s aperture [W/(m2 sr μm)];
- Qcal is the quantized calibrated pixel value (DN);
- Qcalmin is the minimum quantized calibrated pixel value corresponding to Lmin (DN);
- Qcalmax is the maximum quantized calibrated pixel value corresponding to Lmax (DN);
- Lmin is the spectral at-sensor radiance that is scaled to Qcalmin [W/(m2 sr μm)]; and
- Lmax is the spectral at-sensor radiance that is scaled to Qcalmax [W/(m2 sr μm)].
- For commercial satellite systems, essential calibration data are typically provided in header information accompanying image data or at websites describing specific systems and their data.
Estimation of Top of Atmosphere Reflectance
- Accurate measurement of brightness, whether measured as radiances or as DNs, is not optimal because such values are subject to modification by differences in
- Sun angle,
- atmospheric effects,
- angle of observation, and
- other effects that introduce brightness errors unrelated to the characteristics we wish to observe.
- It is much more useful to observe the proportion of radiation reflected from varied objects relative to the amount of the same wavelengths incident upon the object.
- This proportion, known as reflectance, is useful for defining the distinctive spectral characteristics of objects.
Estimation of Top of Atmosphere Reflectance (2)
- Reflectance (Rrs) is relative brightness of a surface, as measured for a specific wavelength interval:
Reflectance=Observed brightness/Irradiance
- As a ratio, reflectance is a dimensionless number (varying between 0 and 1), but it is commonly expressed as a percentage.
- In the usual practice of remote sensing, Rrs is not directly measurable
- because normally we record only the observed brightness and must estimate the brightness incident upon the object.
Estimation of Top of Atmosphere Reflectance (3)
- Reflectance (Rrs) is relative brightness of a surface, as measured for a specific wavelength interval:
Reflectance=Observed brightness/Irradiance
- Radiance is the variable directly measured by remote sensing instruments.
- Radiance is the amount of light the instrument detects from the object being observed.
- When looking through an atmosphere, some light scattered by the atmosphere will be seen by the instrument and included in the observed radiance of the target.
- An atmosphere will also absorb light, which will decrease the observed radiance.
- Reflectance is the ratio of the amount of light leaving a target to the amount of light striking the target.
- Radiance depends on
- the illumination,
- the orientation and position of the target, and
- the path of the light through the atmosphere.
Estimation of Top of Atmosphere Reflectance (4)
- Precise estimation of reflectance would require detailed in situ measurement of wavelength, angles of illumination and observation, and atmospheric conditions at the time of observation.
- Because such measurements are impractical on a routine basis, we must approximate the necessary values.
- Usually, the analyst has a measurement of the brightness of a specific pixel at the lens of a sensor, sometimes known as at-aperture, in-band radiance, signifying that it represents radiance measured at the sensor for a specific spectral channel.
Estimation of Top of Atmosphere Reflectance (5)
- To estimate the reflectance of the pixel, it is necessary to assess how much radiation was incident upon the object before it was reflected to the sensor.
- In the ideal, the analyst could measure this brightness at ground level just before it was redirected to the sensor.
- Although analysts sometimes collect this information in the field using specialized instruments known as spectroradiometers
- typically the incident radiation must be estimated using a calculation of exoatmospheric radiation (ESUNλ) for a specific time, date, and place.
Estimation of Top of Atmosphere Reflectance (6)
QQ = (π × Lλ × d²)/(ESUNλ × cosθ)
- where QQ is the at-sensor, in-band reflectance;
- Lλ is the at-sensor, in-band radiance;
- ESUNλ is the band-specific, mean solar exoatmospheric irradiance;
- θs is the solar zenith angle; and
- d is the Earth–Sun distance (expressed in astronomical units) for the date in question.
- To find the appropriate Earth–Sun distance, some need to generate an ephemeris for the overpass time indicated in the header information for the scene in question.
- The value of d (delta in the ephemeris output) gives the Earth–Sun distance in astronomical units (AU).
Estimation of Top of Atmosphere Reflectance (7)
- Such estimation of exoatmospheric radiation does not, by definition, allow for atmospheric effects that will alter brightness as it travels from the outer edge of the atmosphere to the object at the surface of the Earth.
- However, for many purposes it forms a serviceable approximation that permits estimation of relative reflectances within a scene.
Identification of Image Features
- In the context of image processing, the terms feature extraction and feature selection have specialized meanings.
- “Features” are “statistical” characteristics of image data.
- Feature extraction usually identifies specific bands or channels that are of greatest value for any analysis
- whereas feature selection indicates selection of image information that is specifically tailored for a particular application.
- Thus these processes could also be known as “information extraction”.
Identification of Image Features (2)
- In theory, discarded data contain noise and errors present in original data.
- Thus feature extraction may increase accuracy.
- In addition, these processes reduce the number of spectral channels, or bands, that must be analyzed, thereby reducing computational demands.
- The analyst can work with fewer but more potent channels.
- The reduced data set may convey almost as much information as does the complete data set.
Identification of Image Features (3)
- Multispectral data, by their nature, consist of several channels of data.
- Although some images may have as few as 3, 4, or 7 channels, other image data may have many more, possibly 200 or more channels.
- With so much data, processing of even modest-sized images requires considerable time.
- In this context, feature selection assumes considerable practical significance, as image analysts wish to reduce the amount of data while retaining effectiveness and/or accuracy.
Identification of Image Features - Example
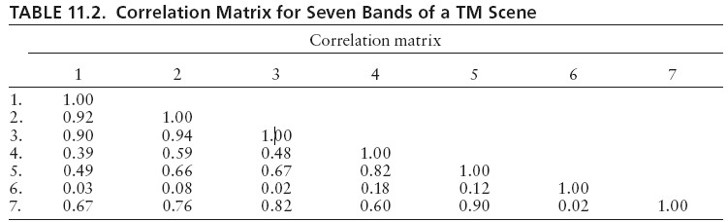
- A variance – covariance matrix shows interrelationships between pairs of bands (TM have 7 bands).
- Some pairs show rather strong correlations — for example, bands 1 and 3 and 2 and 3 both show correlations above 0.9.
- High correlation between pairs of bands means that the values in the two channels are closely related.
- Thus, as values in channel 2 rise or fall, so do those in channel 3; one channel tends to duplicate information in the other.
- Feature selection attempts to identify, then remove, such duplication so that the dataset can include maximum information using the minimum number of channels.
Identification of Image Features - Example (2)
- For data represented by previous Table, bands 3, 5, and 6 might include almost as much information as the entire set of seven channels, because band 3 is closely related to bands 1 and 2, band 5 is closely related to bands 4 and 7, and band 6 carries information largely unrelated to any others.
- Therefore, the discarded channels (1, 2, 4, and 7) each resemble one of the channels that have been retained.
- So a simple approach to feature selection discards unneeded bands, thereby reducing the number of channels.
- Although this kind of selection can be used as a sort of rudimentary feature extraction, typically feature selection is a more complex process based on statistical interrelationships between channels.
Conclusions and take-aways
- soon to be added
Reference list
Barbara Hofer (2018). Innovation in geoprocessing for a Digital Earth. International Journal in Digital Earth.
10.1080/17538947.2017.1379154