Decision Trees

Decision Trees

Decision Trees

  • General Information
  • Decision Trees Components
  • Criteria for nodes splitting
  • Overfitting/underfitting concepts
  • Decision Trees pruning
  • Decision Trees types

General Information

Decision Trees is a supervised non-parametric classifier that takes as input a vector of attribute values and returns a decision

Main characteristics

  • Input/output values can be both numerical and categorical
  • Missing values are allowed
  • Classification structure is explicit and easily interpretable (Friedl & Brodley, 1997)

Decision Trees definition

“A classification procedure that recursively partitions a data set into smaller subdivisions on the basis of a sets of tests defined at each branch (or node)” (Friedl & Brodley, 1997)

Decision Trees example


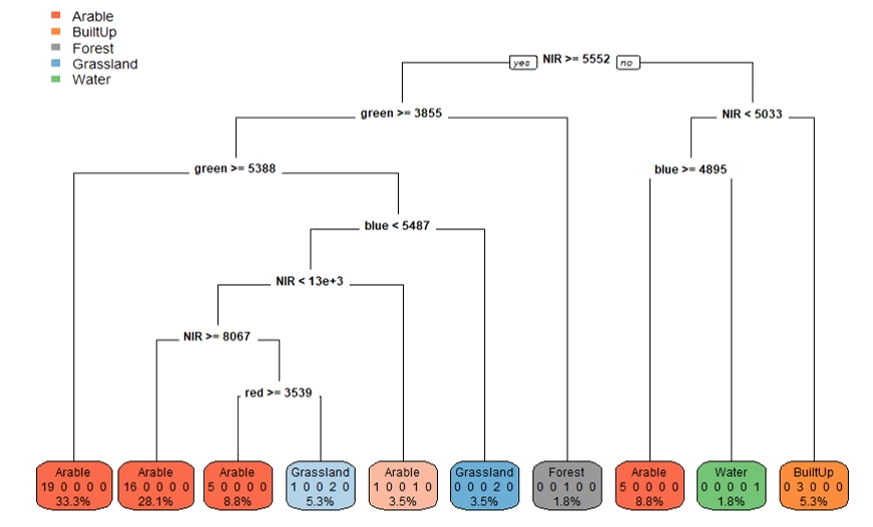Example Decision Trees classification model generated in R using PlanetScope image as input (Digital Number-DN).

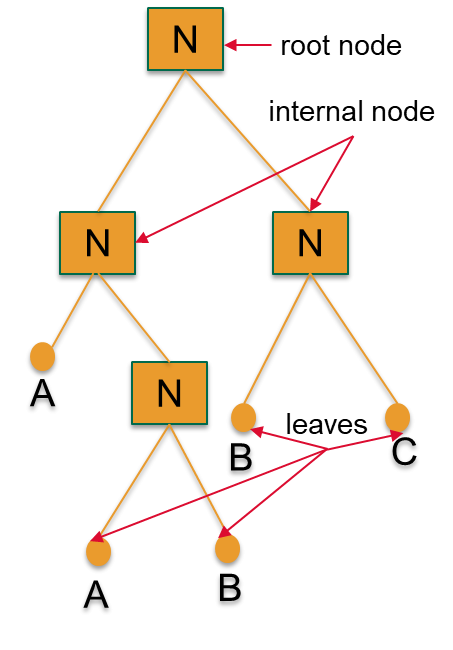
Decision Trees components

  • Nodes: testing different attributes for splitting
  • Edges: connecting to the next node or leaf
  • Leaves: terminal nodes predicting the outcomes

    • DT_Components

Decision Trees types

  • Classification problems: predicting discrete values
  • Regression problems: predicting continuous values

Can you give examples of classification and regression problems?

How to construct Decision Trees?

The mains steps are:

  • select the best attribute as the root node
  • for each value of this attribute, create new child node
  • split samples to child nodes
  • if subset is pure, then terminal node
  • else: continue splitting

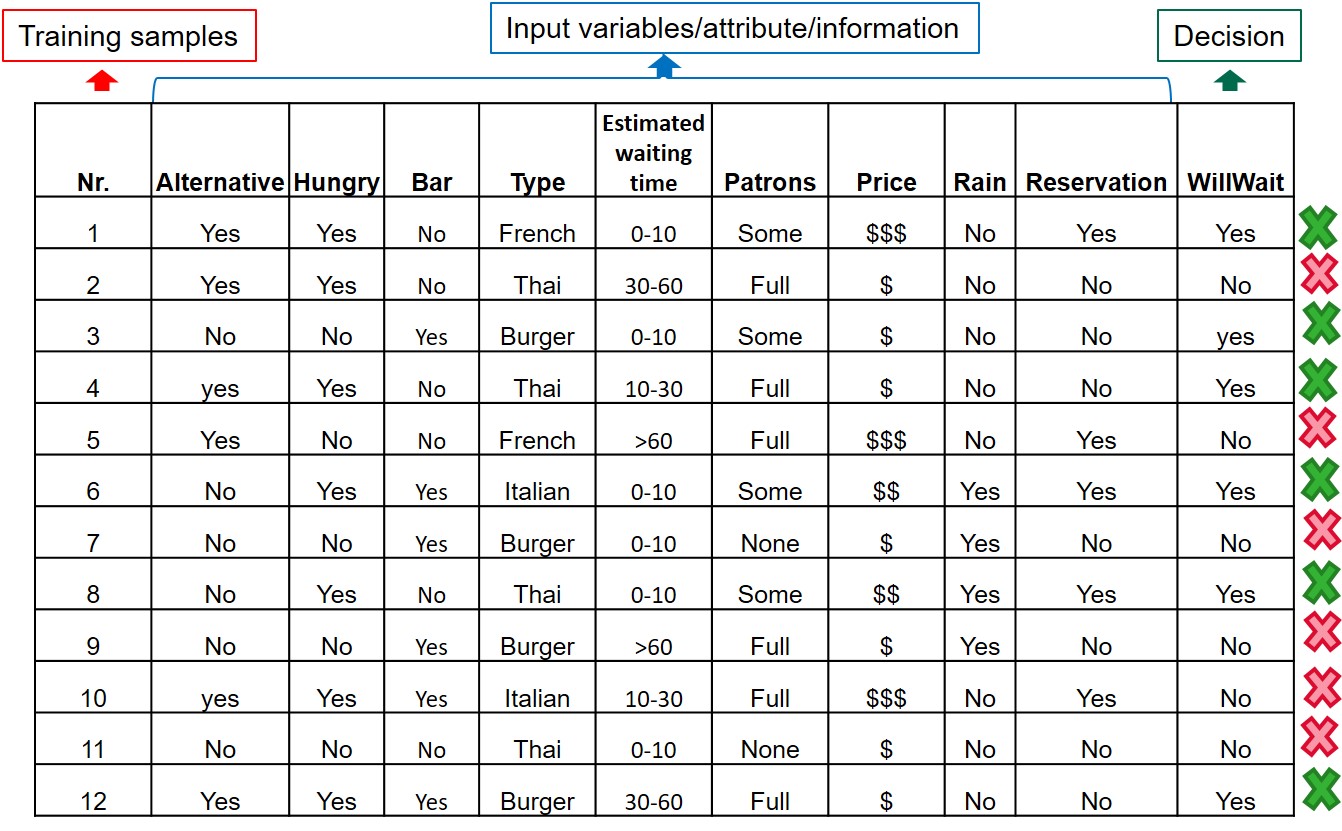
Input variables example


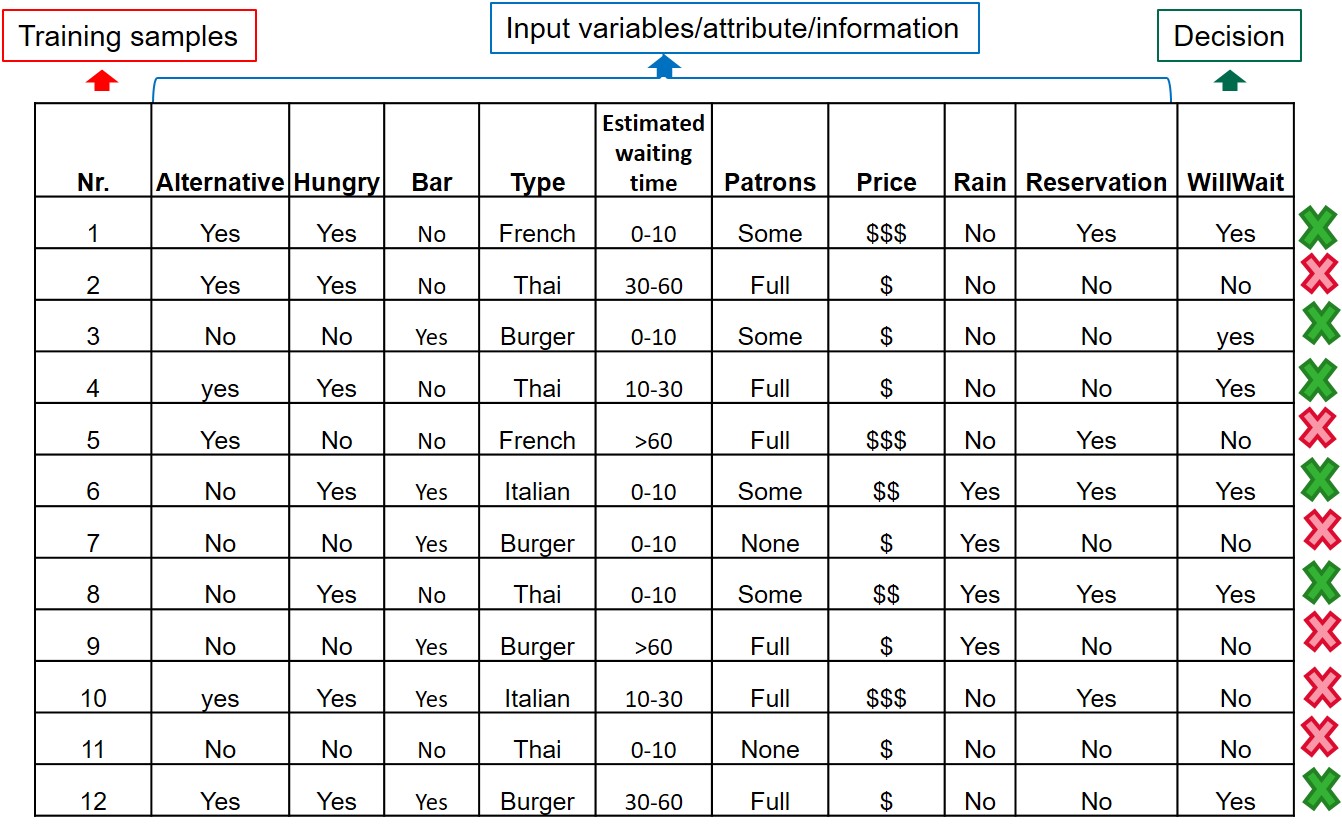Variables Source: Artificial Intelligence: a modern approach (Stuart Russel and Peter Norvig, 2009)

Decision Trees example

(contructed based on the previous presented variables)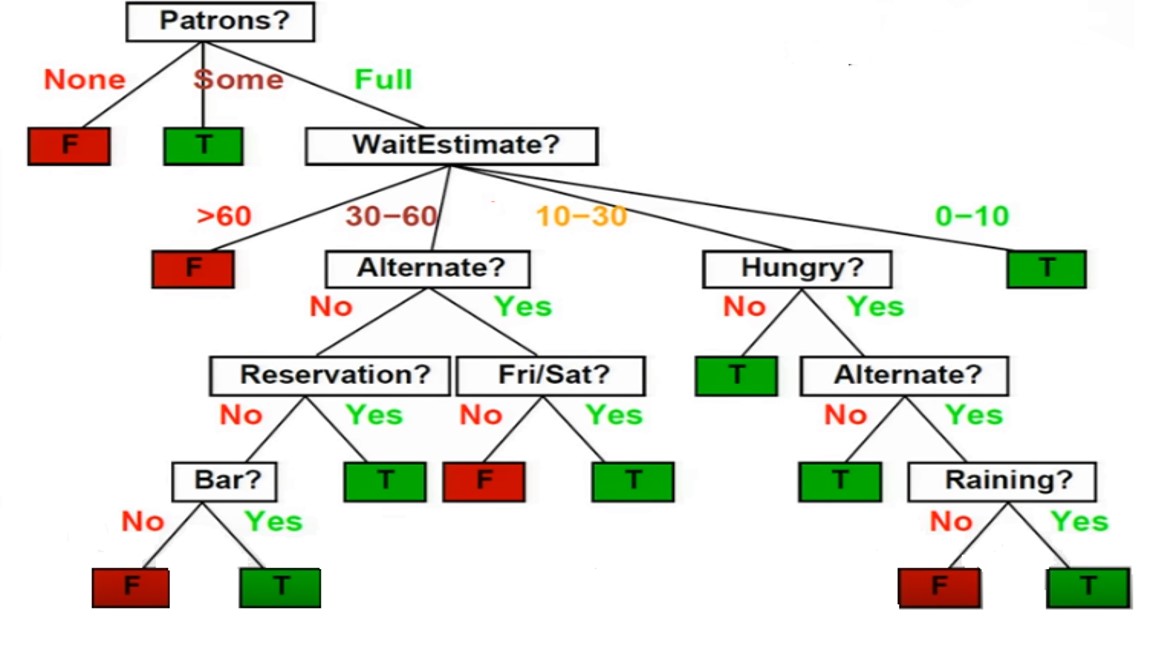
DT_Example Source: Artificial Intelligence: a modern approach (Stuart Russel and Peter Norvig, 2009)

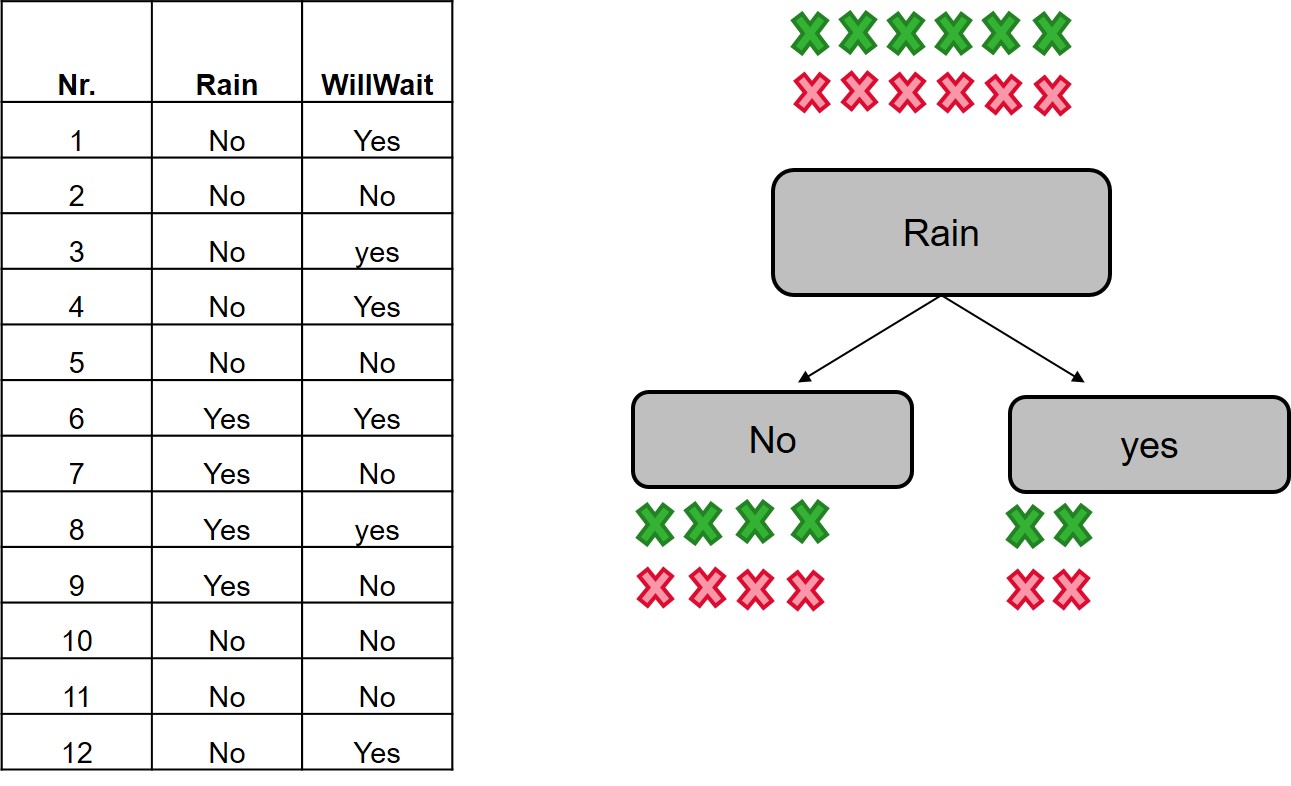
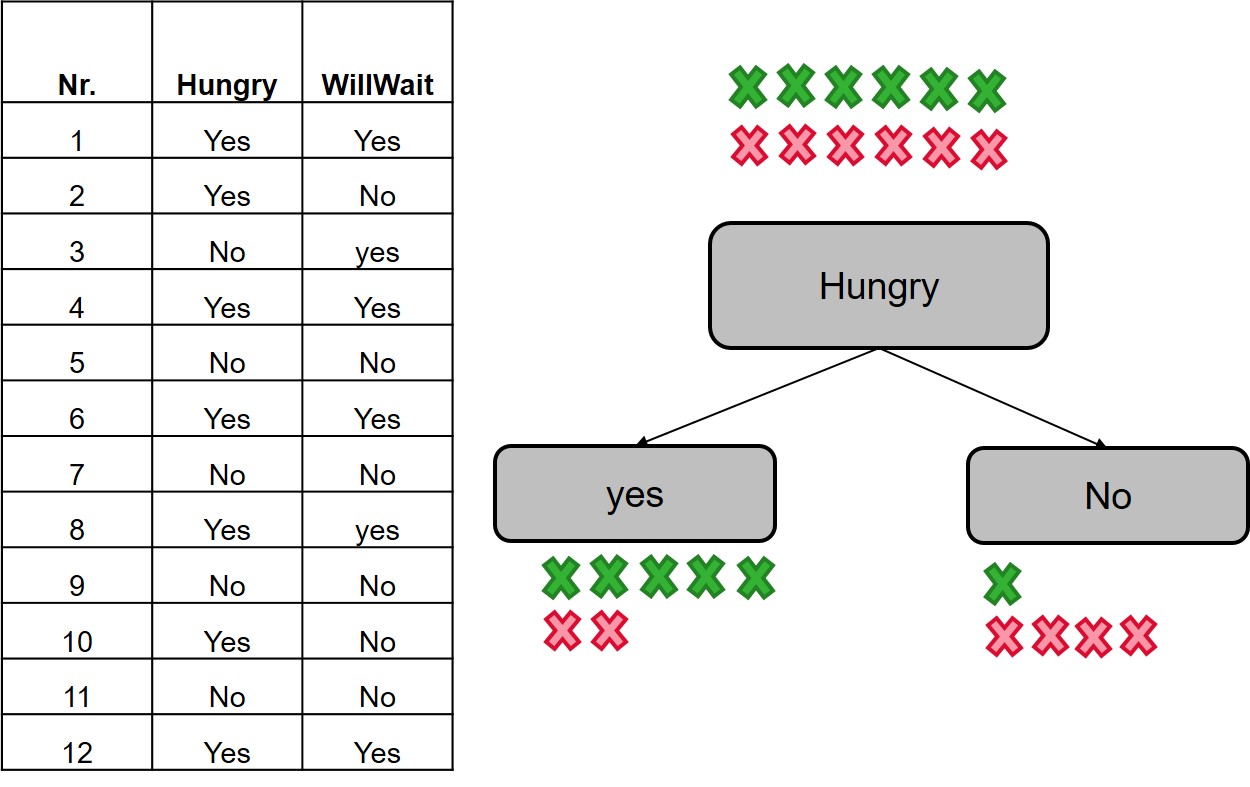
How to select the best variable as the root node?

Patrons variable


OutlookAttribute

Rain variable


RainAttribute

Hungry variable


HungryAttribute

Measures used to split the tree nodes

The splits defined at each internal node of decision trees are estimated from training data by using a statistical procedure

  • Information gain
  • Variance reduction (regression problem)
  • Gini impurity

    • Gini
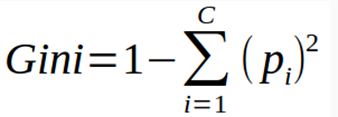
    𝑝𝑖 = probability of an object being classified as a particular class

Information gain

Entropy

  • a measure of uncertainty/how pure a subset/tree node is
  • units used to measure it: bits

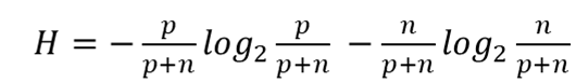
Entropy
p = number of positive examples
n = number of negative examples

Information gain (II)


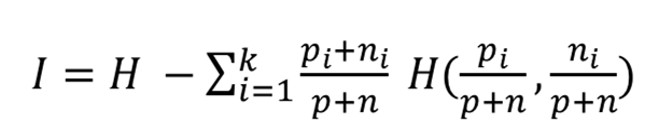
Information Gain
H = entropy
k = values an attribute can take

Calculation of information gain - example

Entropy


InputVariables
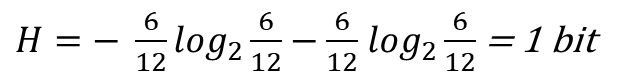
EntropyExample

Calculation of information gain for 'patrons' variable


OutlookAttribute
NoneAtttribute
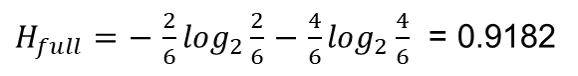
SomeAtttribute
SomeAtttribute

Calculation of information gain for'patrons' variable (II)


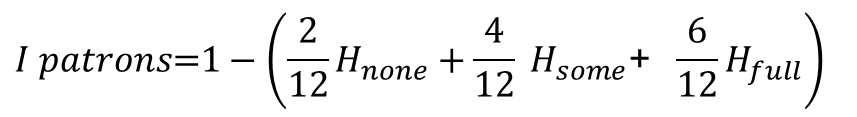
InformationGainPatrons
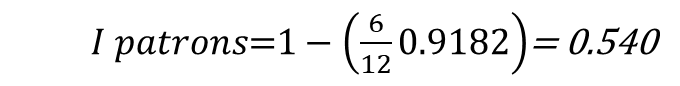
InformationGainPatrons_Final

Calculate the information gain when the variable ‚type‘ is used for splitting the tree nodes

Splitting tree nodes using continuous variables

There are two main options

  • Binay decision = consider all possible splits according to the attributes values (-)
  • Discretization: ordinal categorical feature (+)

Overfitting and underfitting

Overfitting: learning noise on top of the signal

  • Presence of noise
  • Lack of representative samples

Underfitting: the model is too simple to find the patterns in the data

Optimal size of decision trees

Too large: overfitting

  • Poor generalization to new samples (low bias/high variance)

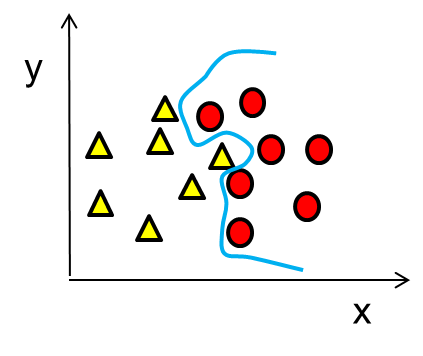
Overfitting
overfitting

Too small: underfitting

  • Poor fit to the data (high bias/low variance)

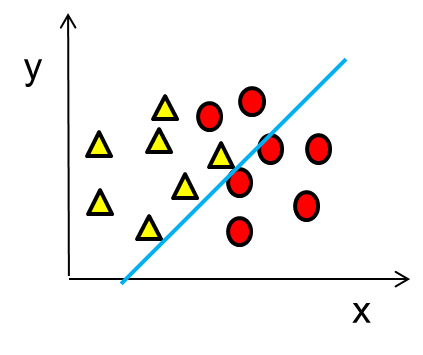
Underfitting
Underfitting

Optimal Decision Trees

  • Do not grow a tree that is too large
  • Pruning: reducing the size of the decision tree

Decision Trees pros and cons

Pros

  • Not a black-box classifier: i.e. users can easily understand the decisions
  • Can handle both categorical and numerical data
  • Can handle missing data
  • Irrelevant attributes are easily discarded
  • fast

Cons

  • Axis-aligned splitting of data

Decision Trees types

'Simple' decision trees

  • Classification and Regression Tree (CART) (Breiman et al., 1984)

Ensemble of Decision Trees (weak learners):

  • Boosting: weighted average of the results
  • Bagging: averaging the results for the end prediction: e.g. Random Forests (Breiman, 2001)

Summary

  • Non-parametric and transparent classifier
  • Addresses both classification and regression problems
  • Different options for splitting the decision trees nodes: information gain, Gini impurity, variance
  • Best decision trees : overfitting/underfitting problems
  • Popular implementations of decision trees: CART, Random Forests

Reference list



Breiman, L. (2001). Random Forest. Machine Learning, 45
Friedl, M.A., & Brodley, C.E. (1997). Decision tree classification of land cover from remotely sensed data. Remote Sensing of Environment, 61, 399-409
Russell, S., & Norvig, P. (2009). Artificial intelligence: a modern approach. (3 edition ed.). Pearson
Slide show ends