Random Forests
What are ensemble classifiers?
Combination of multiple submodels relying on the hypothesis that combining multiple "weak" predictor models together can often produce a powerful model
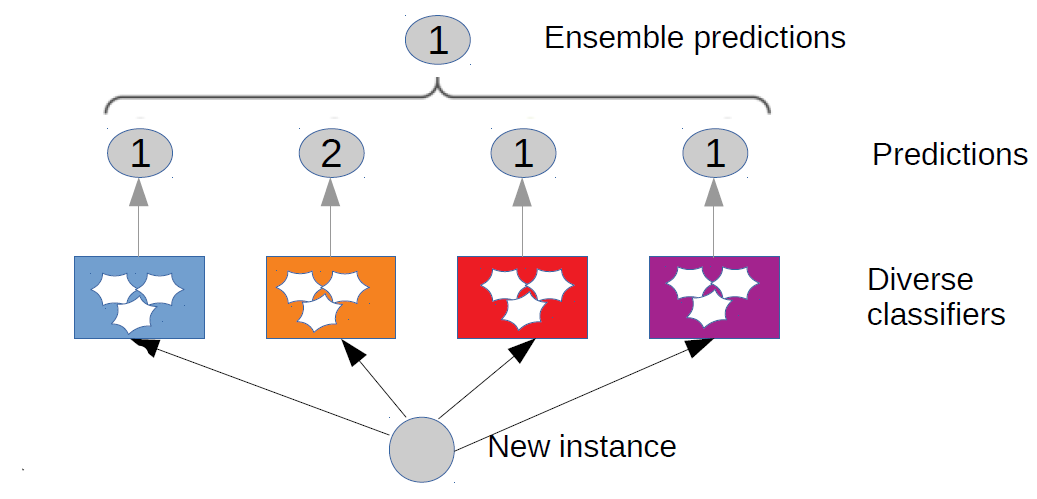
How to create ensemble classifiers?
- Bagging
- Boosting
Ensemble of uncorrelated outcomes
Let's play: pick a random number (A) in range [1, 100].The outcome of the game is:
- Win if A > 40
- Loss otherwise
Game 1: place 100 times, betting $1 each time
Game 2: place 10 times, betting $10 each time
Game 3: place one time, betting $100
We stimulate each game 10000 times. What do you expect?
Game results
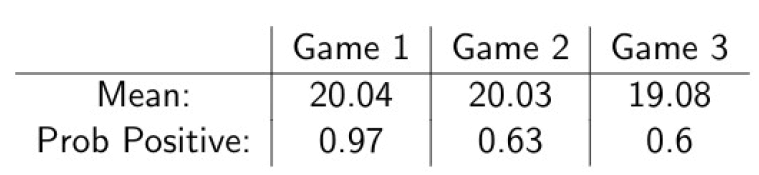
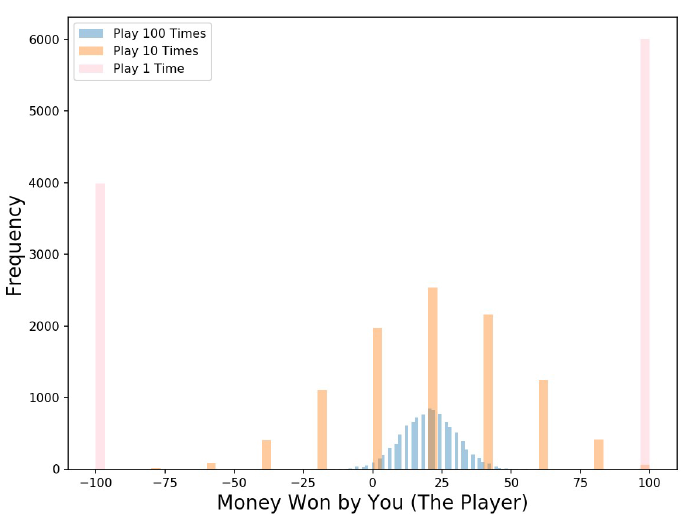
Variance decreases as number of games increases
Bagging (Bootstrap Aggregating)
Suppose we use the same training algorithm for every predictor in the ensemble. However, to train them, we use different random subsets of the training set. The samples are selected randomly with replacement. It means that some samples can be selected seevral times, whereas others might not be selected at all.
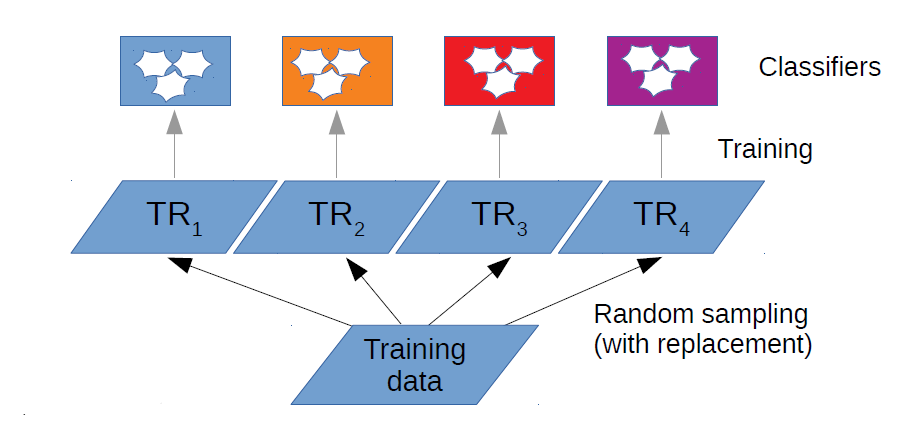
How does this work?
Let's consider the following:
- N = number of samples in training set
- L = number of predictors
- TR = training set for each predictor
- TRi = sample of N randomly selected samples with replacement

Bagging of decision trees
What if these predictors are decision trees?
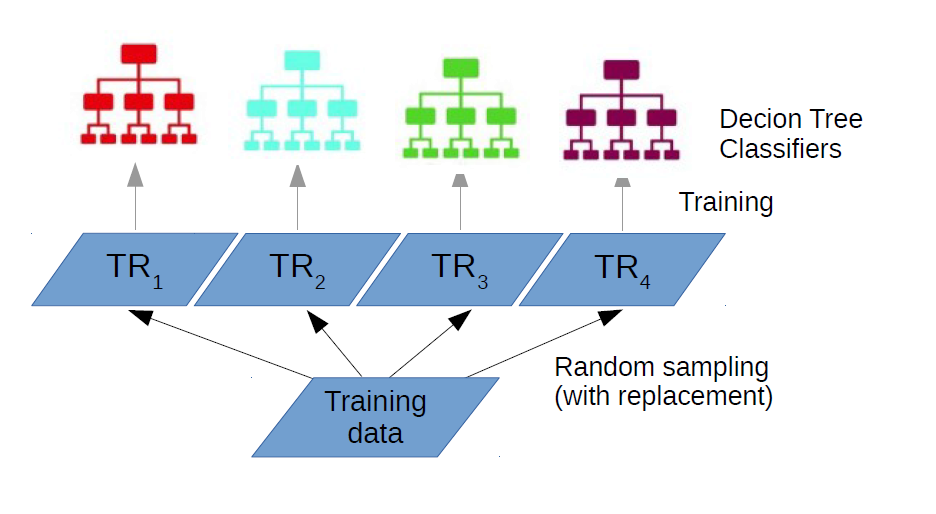
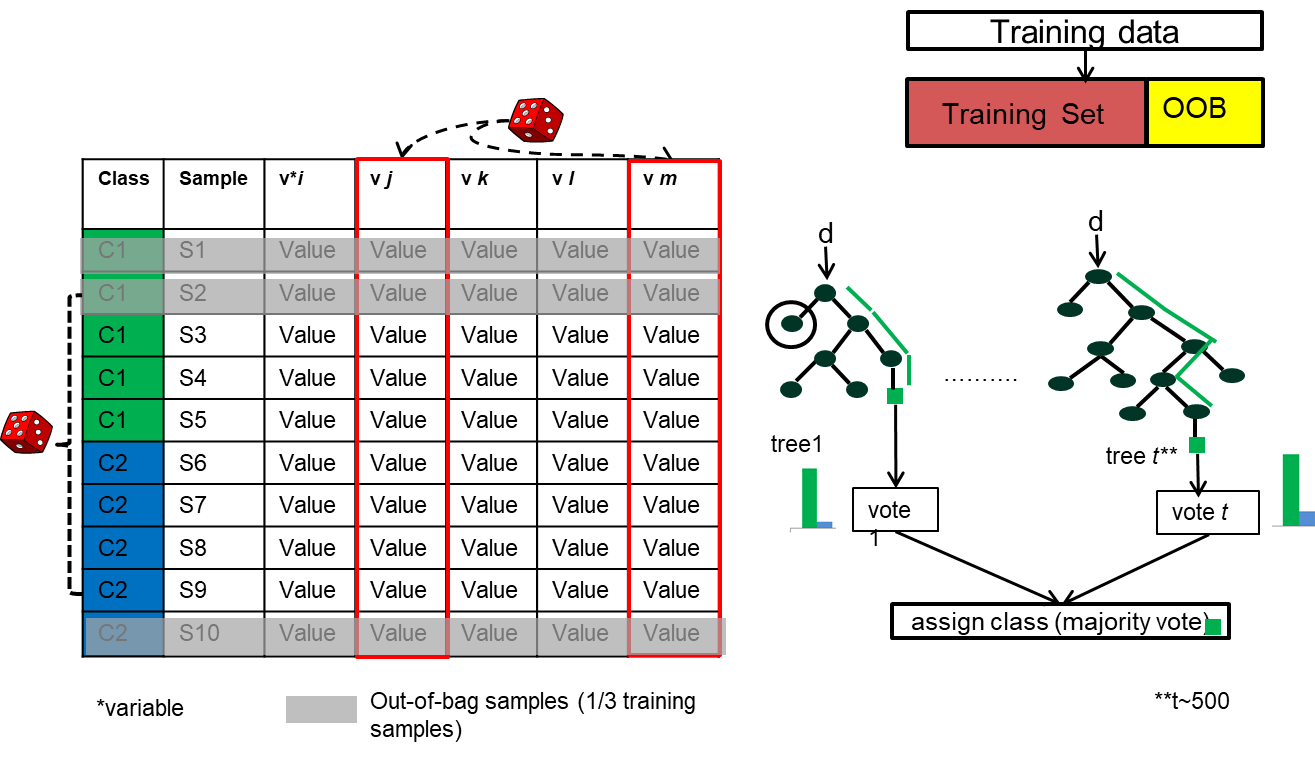
What is Random Forests?
- It is an ensemble of decision trees
- It grows many classification trees (n_estimators)
- Input vector goes through all the trees
- Each tree votes for a class for each input vector
- Class is chosen based on majority of votes
How an individual tree is grown?
From an m number of feature, a max_features are selected randomly at each node. Usually the number of features tested for spliting the tree nodes is represented by the square root of the total number of available features. Each node is split into two nodes only and there is no pruning
How is this procedure different from tree growing in Decision Trees?
Forest error rate
This is highly influenced by:
- Correlation between trees: increasing the correlation increases forest error rate
- Strength of individual forest tree: increasing the tree strength decreases the forest error rate
Forest error rate(2)
Correlation and strength are controlled by max_features. If max_features increases, both correlation between and strength of trees increase. Therefore, we have to find an optimal range of max_features.
Features of Random Forests
The main features of Random Forests are listed below
- It runs efficiently on large data bases
- Not affected by the curse of dimensionality (Hughes phenomenon)
- It gives estimates of what variables are important in the classification
- It is distributed, i.e. each tree can run with a separate subset on a different machine
Out of bag (oob) evaluation
During bagging, approximately one-third of the data samples are left out of TRi. Why?
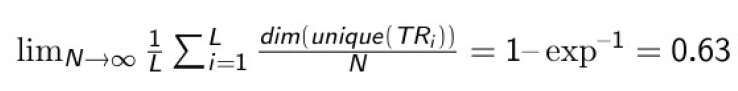
These samples are called out-of-bag (oob) samples.
Why do we need oob?
OOB sample is used for estimating unbiased classification error (oob error estimate) and variable importance
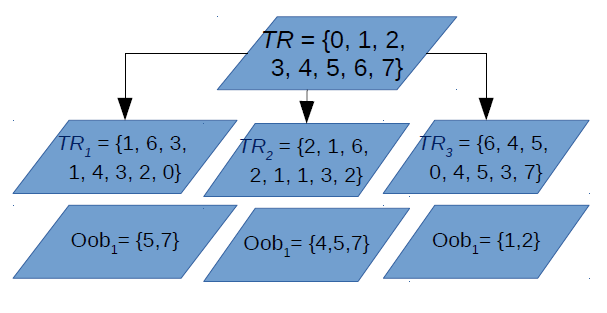
Unbiased oob error estimates
Variable importance
Mean Decrease Accuracy is the commonly used variable importance measure
Let's consider α the number of votes cast for the correct class for all oob samples in all trees. If we permute values of variable m in the oob cases randomly and push them down the tree, then avg(α−β) = raw VI (Variable Importance) score for variable m.
- β = number of cases with correct classification
Proximities
Imagine that you send all training samples (including oob samples) down all trees, count the number of times when sample n and sample k are in the same terminal node and normalize by dividing it by number of trees. What does this tell you?
Random Forests summary (I)
(1) Random Forests is an ensemble classifiers that consists of several decision trees
(2) Decision trees are built by randomly selecting samples through replacement
(3) The most important hyperparamters are the number of decision trees and the number of variables used to split the decision tree nodes
(4) About 1/3 of the samples called out-of-bag samples (OOB) are used for assessing the accuracy of the trained model
(5) OOB is used to calculate the importance of the input variables (e.g. Mean Decrease Accuracy)
Random Forests summary (II)
Reference list
Belgiu, M., & Drǎguţ, L. (2014). Comparing supervised and unsupervised multiresolution segmentation approaches for extracting buildings from very high resolution imagery. ISPRS Journal of Photogrammetry and Remote Sensing, 96, 67-75
Mather, P., & Tso, B. (2009). Classification methods for remotely sensed data (Second Edition), CRC Press
Richards, J. A. (2013). Remote Sensing Digital ImageAnalysis. In Springer. (Section 8.18)